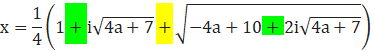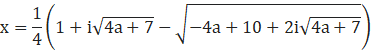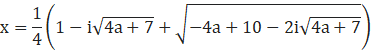令和４年６月26日
[流れ星]
第414回数学的な連続応募解答
＜解答募集期間：5月29日〜6月26日＞
［大垣八幡宮奉納算額7］
岐阜県大垣市にある八幡神社
江戸時代末期、谷松茂（幽斎）は大垣藩士で致道館講官であった水野民興に学び、自ら塾を開いて和算を教えていました。彼の門人達が大垣市の八幡神社に天保年間に算額（絵馬）を奉納しています。この算額は残念ながら先の戦争で神社ごと焼失したことを知り、幽斎算約四編である奉納された算額の解法を後世に残すために、これから32問順に出題していきます。
今回は第13問題から第15問題です。
第13問題
長方形内に正三角形と青円2個と赤円を容れる。青円の直径を知って赤円の直径を求めよ。
出題者 清水何某政高 謹考
第14問題
２個の紫円を黄円に容れ、その間に４個の赤円を容れる。紫円の直径を知って黄円の直径を求めよ。
出題者 清水何某義忠 謹考
第15問題
二等辺三角形に内接する黄円を描き、その間に黒円１個と赤円２個を容れる。赤円と黒円との直径を知って黄円の直径を求めよ。
出題者 中西何某忠充 謹考
追加問題（ジョーカーさん提供）
４次方程式ｘ４―ｘ３＋aｘ２＋ｘ＋１＝０は虚数解αをもち、
（α＋１/α）16＞０のとき、実数aの値を求めよ。
NO1「ジョーカー」 05/29
14時52分 受信 更新 6/26
寄せられた大垣八幡宮奉納算額の第１３問から第１５問、解答です
また、追加問題の解答です.
NO2「よふかしのつらいおじさん」06/12 16時32分 受信 更新 6/26
●赤円の半径をｒ、青円の半径をｂ、正三角形の1辺をｓとします。
・ＡＪの長さは、△ＢＧＨに三平方の定理を用いて、
・ＤＥの長さは、正三角形の辺の半分なので、
・ＥＦの長さは、△ＧＥＦが正三角形の半分なので、
・ＣＤの長さは、正三角形の高さなので、
●
・ＡＪ＝ＤＦ＝ＤＥ＋ＥＦより、
・ＡＤ＝ＡＣ＋ＣＤ＝ＪＦより、
よって、
第14問題
●各円の半径を、紫円:ｍ、黄円:ｙ、赤円:ｒとします。
・ＣＤの長さは、△ＣＤＦに三平方の定理を用いて、
ＣＥ＝ＣＤ＋ＤＥなので、
・ＣＤの長さは、△ＣＤＧに三平方の定理を用いると、
ＣＥ＝ＣＤ＋ＤＥなので、
ゆえに、
第15問題
●各円の半径を、黒円:ｂ、黄円:ｙ、赤円:ｒとします。
・ＢＣの長さは、第13問題より、
・ＣＤ(ＫＨ)の長さは、第13問題より、
・△ＡＢＦ∽△ＡＣＧなので、
・△ＥＤＪ∽△ＥＣＧなので、
●△ＡＦＢ∽△ＡＥＨなので、
追加問題
●
が正(実数)になるのは、
の偏角
が、
の倍数になるときです。
なぜなら、2つの複素数の積は偏角がそれぞれの偏角の和になるからです。
●
この4次方程式の解に0はありません。
よって、
を調べます。
とおくと、
のとき、方程式は実数解をもちます。
のとき、方程式は虚数解をもちます。
●
として考えます。
1)
とすると、
ゆえに、
2）
とすると同様に、
ゆえに、
3)
とすると同様に、
ゆえに、
4)
とすると同様に、
ゆえに、
1)、2)の場合、互いに逆数の和を2乗すると、
3)、4)の場合、互いに逆数の和を2乗すると、
この形だと、
の形になり複素平面で考えやすくなります。
・偏角が
に関係するときは、（実部の絶対値＝虚部の絶対値）です。
このaはともに、
をみたします。
・偏角が
に関係するときは、純虚数なので実部が0です。
これも条件をみたします。
・偏角が180°に関係するときは、実数なので虚部0が必要条件です。
よって、
これは条件をみたしません。
●2乗の複素数を図示します。
するとその8乗の複素数が、正の実数になるのがわかります。
・
のとき、
・
のとき、
NO3「三角定規」 06/25
19時10分 受信 更新 6/26
寄せられた第１５問の解答です。
皆さん、問題や質問に答えてください。一部でも構いませんから、解答とペンネームを添えて、メールで送ってください。待っています。
