�ߘa�V�N10��12��
 [���ꐯ]
[���ꐯ]
�@�@��459�����w�I�ȘA�������
�@�@�@����W���ԁF�X��14���`10��12����
�m��ʍ����������~�Q�̗ݏ�ł��鐔��̘a�n

�lj�����i�o��҂́u�W���[�J�[�v�j�@�V��V���[�Y
�l���~���̐����`�Ɛ��O�p�`��1�ӂɂ��āw�Q�x�@
���P�@�@�V���[�Y5���
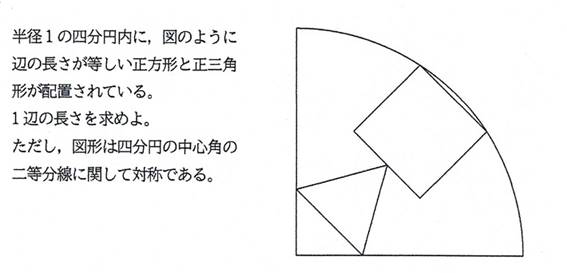
�����`�Ɛ��O�p�`��1�ӂ��������Ƃ�(�ӂ����L���Ȃ�),
���Q�@�V���[�Y6���
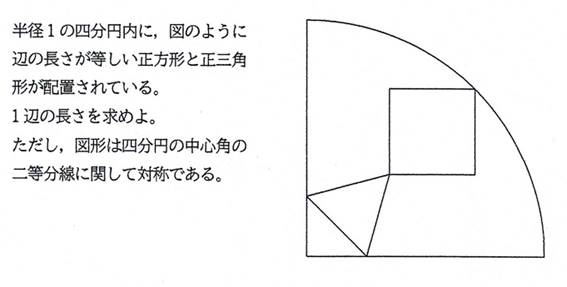
�����`�Ɛ��O�p�`��1�ӂ��������Ƃ�(�ӂ����L���Ȃ�),
NO1�u�W���[�J�[�v �@ 09/14�@�@ 21��30�� ��M �X�V 10/12
��ꂽ������
NO2�u�X���[�N�}���v 09/15 00��53���@ ��M �X�V 10/12
���[�͗��ɏH�̋C�z���Y���悤�ɂȂ�A�����ԉ߂����₷���Ȃ�܂�����
������G�n�̕��͉����܂��� ^^
NO3�u���j���w�ҁv �@ 09/15 9��56���@ ��M �X�V 10/12
�������̌v�Z�ƘA���P���������̉��ƌ��ʂ̊m�F�ɂ��ẮA�v�Z�@���g�p���܂����B
�m��ʍ����P�����~�Q�̗ݏ�ł��鐔��̘a�n�̉�
�u���j���w�ҁv �@ 09/19 11��01���@ ��M
�X�V 10/12
��459�w�I�ȘA��������ł́A�Q�̗ݏ�̏ꍇ�ł������A
�������@�ŁA3,4,(1/2)�̗ݏ�̏ꍇ���A�v�Z���Ă݂܂����B���ʂ͈ȉ��̒ʂ�ł��B�O��̂ƈꏏ�ɂ��܂����B
�m��ʍ����P�����~�Q�̗ݏ�ł��鐔��̘a�n�̉�
NO4�u�O�p��K�v 09/15 18��40���@
��M �X�V10/12
��ꂽ������
NO5�u��ӂ����̂炢��������v09/17 23��11����M �X�V 10/12
�@�@��ꂽ������
NO6�ur-de-r�v�@�@ 09/20�@ 14��28�� ��M �X�V 10/12
�@�@��ꂽ������
NO7�ukasama�v 09/22 00��37���@ ��M
�X�V 10/12
��ꂽ������
����̐��w�I�ȘA��������̉��A�����肢�����܂��B
����I�ȉ�@�͕����т܂���ł������A�v�Z�ʂ����炷�H�v�����Ă݂܂����B
NO8�u�l�c�����v�@�@�@ 09/26 17��01���@
��M �X�V 10/12
��ꂽ������
NO9�u��x�Ђ����v 09/28 14��18���@
��M �X�V 10/12
��459��m��ʍ����P�����~�Q�̗ݏ�ł��鐔��̘a�n
(�T)�`(�X)�̉�
(�T)��[k=1,n](k^1)*(2^k)=(2^(n+1))*(n-1)+2
(�U)��[k=1,n](k^2)*(2^k)=(2^(n+1))*(n^2-2*n+3)-6
(�V)��[k=1,n](k^3)*(2^k)=(2^(n+1))*(n^3-3*n^2+9*n-13)+26
(�W)��[k=1,n](k^4)*(2^k)=(2^(n+1))*(n^4-4*n^3+18*n^2-52*n+75)-150
(�X)��[k=1,n](k^5)*(2^k)=(2^(n+1))*(n^5-5*n^4+30*n^3-130*n^2+375*n-541)+1082
�ȉ��ŁCS2(m,r)�͑�2��X�^�[�����O����\�����̂Ƃ���D���Ȃ킿�C
S2(m,r)=(1/r!)*��[j=0,r]((-1)^j)*binomial(r,j)*(r-j)^m
�ł���Ƃ���D
�C�ӂ̐����� n,m ����� x��1 �Ȃ�C�ӂ̎��� x �ɑ��āC
�a ��[k=1,n](k^m)*(x^k) �͎����Ōv�Z�ł���D
��[k=1,n](k^m)*(x^k)
=(x^(n+1))*��[r=1,m]S2(m,r)*(-r!)*(��[j=0,r]binomial(n+1,j)*(x^(r-j))*(1-x)^(-r+j-1))
+��[r=1,m]S2(m,r)*(r!)*(x^r)*(1-x)^(-r-1).
����x=2�̂Ƃ��ɂ͎��̂悤�ɂȂ�D
��[k=1,n](k^m)*(2^k)
=(2^(n+1))*��[r=1,m]S2(m,r)*(r!)*(��[j=0,r]binomial(n+1,j)*(-2)^(r-j)) - ��[r=1,m]S2(m,r)*(r!)*(-2)^r.
(�ؖ�)
t���Cx*t��1�Ȃ�ϐ��Ƃ��C
F(n,x,t)=��[k=0,n](x^k)*(t^k)�C
a(n,m,x,t)=��[k=0,n](k^m)*(x^k)*(t^k)�@�Ƃ���D
F(n,x,t)
=1+x*t+(x*t)^2+(x*t)^3+ �c +(x*t)^n
=(1-(x*t)^(n+1))*(1-x*t)^(-1) ---(��)
�ł���D
t�̊�G(t)�ɑ��āCG(t)��t�ŁCr�������������̂� Diff(G(t),t,r)
�Ƃ������Ƃɂ���ƁC
Diff(F(n,x,t),t,r)
=��[k=0,n]k*(k-1)*(k-2)*�c*(k-r+1)*(x^k)*t^(k-r)
=��[k=0,n]binomial(k,r)*(r!)*(x^k)*t^(k-r).
�܂��C(��)�ɒ��ӂ���ƁC���C�v�j�b�c�̖@�����CDiff(F(n,x,t),t,r)��
���̂悤�ɂ�������D
Diff(F(n,x,t),t,r)
=��[j=0,r]binomial(r,j)*Diff((1-(x*t)^(n+1)),t,r-j)*Diff((1-x*t)^(-1),t,j).
����ɁC��2��X�^�[�����O�� S2(m,r) ��p����ƁCk^m ��
���̂悤�ɂ����邱�Ƃɒ��ӂ���D
k^m
=��[r=1,m]S2(m,r)*k*(k-1)*(k-2)*�c*(k-r+1)
=��[r=1,m]S2(m,r)*binomial(k,r)*(r!).
�ȏォ��Ca(n,m,x,t)�͎��̂悤�ɕό`�ł���D
a(n,m,x,t)
=��[k=0,n](k^m)*(x^k)*(t^k)
=��[k=0,n](��[r=1,m]S2(m,r)*binomial(k,r)*(r!))*(x^k)*(t^k)
=��[r=1,m]S2(m,r)*��[k=0,n]binomial(k,r)*(r!)*(x^k)*(t^k)
=��[r=1,m]S2(m,r)*(t^r)*Diff(F(n,x,t),r)
=��[r=1,m]S2(m,r)*(t^r)*��[j=0,r]binomial(r,j)*Diff((1-(x*t)^(n+1)),t,j)*Diff((1-x*t)^(-1),t,r-j)
=((x*t)^(n+1))*��[r=1,m]S2(m,r)*(-r!)*��[j=0,r]binomial(n+1,j)*((x*t)^(r-j))*(1-x*t)^(-r+j-1)
+��[r=1,m]S2(m,r)*(r!)*((x*t)^r)*(1-x*t)^(-r-1).
����āC��[k=1,n](k^m)*(x^k)�͎��̂悤�ɂ�����D
��[k=1,n](k^m)*(x^k)
=��[k=0,n](k^m)*(x^k)
=a(n,m,x,1)
=(x^(n+1))*��[r=1,m]S2(m,r)*(-r!)*(��[j=0,r]binomial(n+1,j)*(x^(r-j))*(1-x)^(-r+j-1))
+��[r=1,m]S2(m,r)*(r!)*(x^r)*(1-x)^(-r-1).
(�ؖ��I)
m=1�`50�ɑ��ẮC��[k=1,n](k^m)*(2^k)�� n �̎��ŕ\�������̂��C
���L�y�[�W�ɓ\��t���Ă����܂����D
�v�Z�� wxMaxima �ōs���܂����D
https://fpseries.exblog.jp/33789478/
�����̗���F��L�̃T�C�g��q�����܂����B���̌��ʂ͈�̍��Y�ɂȂ�܂��B�[���l�@�Ɋ��ӂ��܂��B�������܂����B��
[�lj����1]
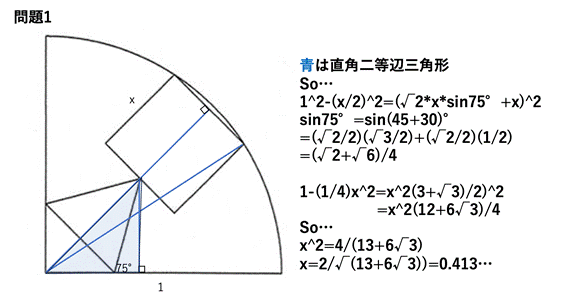
��ӂ̒����́C2/(13+6*3^(1/2))^(1/2)
(��)
��ӂ̒�����s�Ƃ���ƁC
((s/2)+(s/2)*3^(1/2)+s)^2+(s/2)^2 = 1^2.
����āCs=2/(13+6*3^(1/2))^(1/2).
[�lj����2]
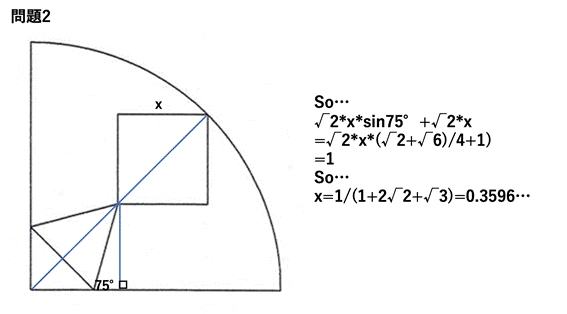
��ӂ̒����́C(2*2^(1/2)-3)*3^(1/2)+4*2^(1/2)-5
(��)
��ӂ̒�����t�Ƃ���ƁC
(t/2)+(t/2)*(3^(1/2))+t*(2^(1/2))=1.
�����,
t=2/(1+2*2^(1/2)+3^(1/2))
=(2*2^(1/2)-3*3^(1/2)+4*2^(1/2)-5.
(�ȏ�)
�u��x�Ђ����v 10/09 08��21���@ ��M �X�V 10/12
�a
��[k=1,n](k^m)*(x^k)�� n �̎��ŕ\���ʖ@�F
Diff( , , ), S2(m,r) �Ȃǂ̈Ӗ��͐�̂��̂Ɠ����ł��D
Diff((x*e^t)^k,t,m)=(k^m)*(x^k)*e^(k*t) �ł��邱�Ƃɒ��ӂ���ƁC
(k^m)*(x^k)=lim[t��0]Diff((x*e^t)^k,t,m).
����āC
��[k=1,n](k^m)*(x^k)
=��[k=0,n](k^m)*(x^k)
=��[k=1,n]lim[t��0]Diff((x*e^t)^k,t,m)
=lim[t��0]��[k=0,n]Diff((x*e^t)^k,t,m)
=lim[t��0]Diff(��[k=0,n](x*e^t)^k,t,m)
=lim[t��0]Diff((1-(x*e^t)^(n+1))*(1-x*e^t)^(-1),t,m)
=lim[t��0]��[r=0,m]binomial(m,r)*Diff(1-(x*e^t)^(n+1),t,m-r)*Diff((1-x*e^t)^(-1),t,r)
=lim[t��0]��[r=0,m]binomial(m,r)*(-(n+1)^(m-r)*(x*e^t)^(n+1))*��[j=0,r](-1)^(j+r)*(j!)*S2(r+1,j+1)*(1-x*e^t)^(-j-1)
=x^(n+1)*��[r=0,m](binomial(m,r)*(n+1)^(m-r)*(-1)^r*��[j=0,r](j!)*S2(r+1,j+1)*(x-1)^(-j-1))
-��[j=0,m](-1)^m*(j!)*S2(m+1,j+1)*(x-1)^(-j-1).
���� x=2 �̏ꍇ�ɂ́C
��[k=1,n](k^m)*(2^k)
=2^(n+1)*��[r=0,m](binomial(m,r)*(n+1)^(m-r)*(-1)^r*��[j=0,r](j!)*S2(r+1,j+1))
-��[j=0,m](-1)^m*(j!)*S2(m+1,j+1).
a(n,m,x)=��[k=1,n](k^m)*(x^k)�Ƃ��āCwxMaxima�Ōv�Z����ꍇ�ɂ͈ȉ��ł��D
a(n,m,x):=x^(n+1)*expand(sum(binomial(m,r)*(n+1)^(m-r)*(-1)^r*sum(j!*stirling2(r+1,j+1)*(x-1)^(-j-1),j,0,r),r,0,m))-sum((-1)^m*j!*stirling2(m+1,j+1)*(x-1)^(-j-1),j,0,m);
S2(m,r)�̓V�O�}�a�ł�����̂ŁC��L�̃�[k=1,n](k^m)*(x^k)�́C�V�O�}�̎O�d�a
�Ƃ������ƂɂȂ�܂��D�v�Z�͂��Ȃ�ʓ|�ł��D
���̃V�O�}�̎O�d�a������ɊȖ�ł���̂��ۂ��C���ɂ͂킩��܂���ł����D
(�ȏ�)
���ʁ@8��9���ɑ�w�̓������A���̖���b��ɂ����Ƃ���A����@���������牺�L�̂悤�ȍl�@�������Ă��܂����B


�����̗��ꁄ�@�@�@�@�@�@�@�@�@�@�@�@�@�@�X�V�@�@10��12��

�����̗���F���̖�肪�����܂Ŕ��W�g�����ꂽ�F�l�̐[���l�@�ɂ͖ڂ���������̂�����܂����B�o��҂Ƃ��Ă͊���������ł��B���傳�ꂽ��@�ɂ͊����̘A������ł����B����҂̊F�l�Ɍh�ӂ�\���܂��B���߂Đ[�����Ӑ\���グ�܂��B��