令和７年１０月１２日

[流れ星]

　　第460回数学的な連続応募問題

　　　＜解答募集期間：10月12日〜11月11日＞

［三角形の面積の二等分

＋NHKの算額］

　

　三角形ＡＢＣにおいて,ＡＢ≧ＡＣとする。辺ＢＣ上の点Ｐより垂線を引き,

辺ＡＢの交点をＱとする。このとき,垂線ＰＱは三角形ＡＢＣの面積を二等分している。ただし,三辺の長さをＢＣ＝ａ,ＣＡ＝ｂ，ＡＢ＝ｃとする。

設問１　辺ＢＰの長さをａ，ｂ，ｃで表せ。

設問２　点Ｐを作図せよ。

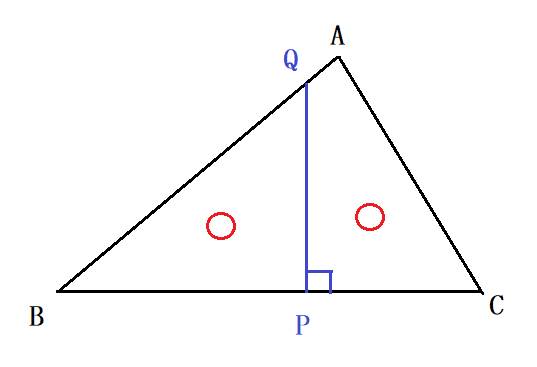
お願い：設問２の点Ｐの作図方法が分かりません。教えてください。

別問題　＜9月2日(火)NHK総合TV午後11時からの「最深日本研究　和算　算額」で放送問題＞　

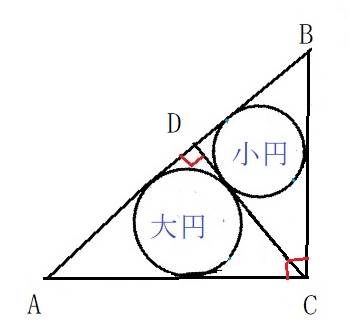
∠C=90°の直角三角形ＡＢＣにおいて,点Ｃから斜辺ＡＢに図のように垂線ＣＤを引く。△ＡＣＤ、△ＢＣＤの内接円を大円、小円とする。大円,小円の直径をそれぞれ、３２尺,２４尺としたとき, 直角三角形ＡＢＣの３辺の長さを求めよ。

追加問題（出題者は「ジョーカー」）　新作シリーズ

四分円内の正方形と正三角形の1辺について『２』　

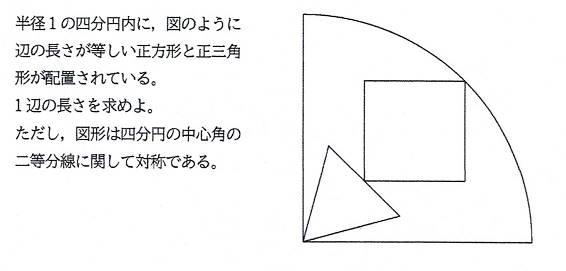
問題１　　シリーズ7問目

正方形と正三角形の1辺が等しいとき(辺を共有しない),

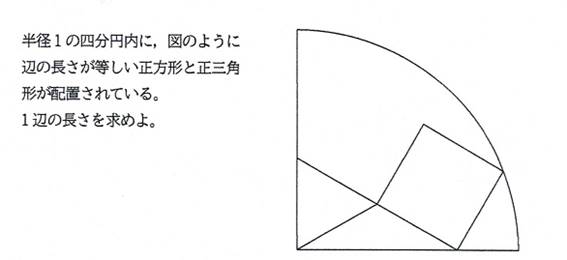
問題２　シリーズ8問目

正方形と正三角形の1辺が等しいとき(辺を共有しない),

皆さん、問題や質問に答えてください。一部でも構いませんから, 解答とペンネームを添えて, メールで送ってください。待っています。